Kiahna's Scribe Post

Algebra Problem Solving!!
1. Mr. Enigma said, five less then one fourth of my age is 12 how old is Mr. Enigma?
Mr Enigma is 68 years old. Let x=his age
we are going to make x=1 becasue you can do that. they answer is

x/4-5=12
+5 +5
(4)x/4 17(4)
x= 68

2. Suppose you have $40 and you earn $7 per hour. How many hours must you work untill you have $131?
You would have to 28 work hours
7x+40=131
-40 -40
7x/7 91/7
x=28

3. Valley video charges a $15 annual fee plus $3 per movie for rentals. Last year, Jennifer spent $99 at the store. How many movies did she rent?
She rented 99 movies?
3x+15=99
-15 -15
3x/3 84/3
x=28

5.Suppose you are salesperson for Quark Compuer Company. Each month you earn $500 plus one sixth of your sales. What amount must you sell this month to earn $3000?
The amount he would have to sell was 15000.
x/6+500=3000
-500 -500
(6) x/6 2,500(6)
x= 15,000
6. For lunch Dregg had a hamburger and potato chips. The hamburger had 325 calories and each chip had 12 calories. If the meal had 541 calories, how many chips did Dregg eat?
He ate 18 chips.
12x+325=541
-325 325
12x/12 216/12
x=18

Robby's Scribe

Today in class, we got this algebra work sheet. So, I'll do some of the questions on the number-answer sheet, not geometry side.

Question 1:

The second of two numbers is 4 times the first. Their sum is 50. Find the numbers.

Ok, so, to answer this question, we have to find out which is the variable and have it equal 50. It also says "sum", so there is going to be addition in this question.
To find the variable, you have to read the sentence and find out what part of the question isn't told. But first, write the simple-sentence answer, which is just the answer in a sentence. You write this out first, then come back to it once u find the numbers.

10 40
The numbers are ____ and ____. (You can also write this at the end of the equation, which is what I'm going to do just to make it make more sense.)

"The second of two numbers"
This means that, in the equation, the second number will NOT be the variable, because if u read on..."is 4 times the first". This means it will be 4x, not just x, which is what we need.
So the first number will be x.
Remember, you have to have the "Let X = blahblah" somewhere in that equation, or u lose marks.

Moving on, 4x would be on the right side of the + sign, because it is the second number. The first number is x.
So the equation would look like this:
Let x = First number
x + 4x = 50 (what we have so far)
5x = 50 (combined like terms)
-- ---
5 5
x = 10
The answer to this question would be 10, 40.

SUBSTITUTE TO CHECK (this is to make sure you have the right answer)
x + 4x = 50 (must write formula)
10 + 4(10) = 50
10 + 40 = 50
50 = 50

x = 10
4x = 40 (this is very important too, before you write your answer into the sentence, you have to write out what the variable and term stand for in numbers, like above. Now you see why its easier to write the sentence at the bottom)

If the answer on the left side equals the right side (50 = 50), that means the number works.

Question 2:

(I will now be writing all the answers out with some info in brackets, if you don't get it, go back to Question 1: and read on how to get it.)

The larger of two numbers is 12 more than the smaller. Their sum is 84. Find the numbers.

"Larger of two numbers is 12 more than smaller"

The two other numbers would equal x, because nothing is told about them.

Let x = Smaller Number 1, Smaller number 2.

x + 12 + x + x = 84
3x + 12 = 84 (combined like terms)
-12 -12
3x = 72
-- ---
3 3
x = 24

Substitute to Check:

x + 12 + x + x = 84
3(24) + 12= 84
72 + 12 = 84
84 = 84

x+12 = 36
x = 24
x = 24

36 24 24
The numbers are ____, ____, and ____.

The answer would be 36, 48 [because 36 is 24 + 12 and 48 is 24 + 24 (2 x 24)]

Question 4:

The second of two numbers is 5 more than twice the first. Their sum is 80. Find the numbers.


"second of two numbers"
So the second number would be the term (number with the x or a or whatever letter next to it)
and the first number would be the variable.

Let x = First Number

"5 more than twice the first"
2x + 5
"sum is 80"
= 80
Now put it al together...

x + 2x + 5 = 80
3x + 5 = 80
- 5 -5
3x = 75
-- ---
3 3

x = 25

Substitute to Check:

x + 2x + 5 = 80
3(25) + 5 = 80
75 + 5 = 80
80 = 80

2x+5 = 55
x = 25
25 55
The numbers are _____, and _____.
25, 55.

Question 6:

Find two numbers whose sum is 92, if the first is 4 more than 7 times the second. Find the First number.

"Two numbers whose sum is 92, if the first is 4 more than 7 times the second"
so the second number is x, because it doesn't mention anything about it.

Let x = Second Number

(7x + 4) + x = 92 (brackets there to make it look simpler)
8x + 4 = 92 (combined like terms)
- 4 -4
8x = 88
-- --
8 8
x = 11

Substitute to check:

(7x + 4) + x = 92
8(11) + 4 = 92
88 + 4 = 92
92 = 92

x = 11
7x + 4 = 81

The first number is 11.

Question 8:

Together, a necklace and a bracelet cost $192. Find the price of each if the necklace costs 3 times as much as the bracelet.

"if the necklace costs 3 times as much as the bracelet"

This means the bracelet is x.
Let x = bracelet

3x = Necklace

3x + x = 192
4x = 192
-- ----
4 4
x = $48 ($48.00)

Substitute to check:

3x + x = 192
4(48) = 192
192 = 192

(now to find the price of a necklace and bracelet separately)

3x = 3(48)
= 144
x = 48

$144.00
+$48.00
--------
$192.00

The price of a bracelet is $48.00 and the necklace is $144.00.

Romulo's Scribepost

SCRIBE POST

So today in math we first went over this math sheet we had for homework called 7.3 Solving Geometric Problems. This took up about 45 minutes of the class and for the rest of the class we had time to do some of our homework which I'm scribing today.


Since no one has scribed anything about Algebra problem solving I'll post the 6 steps.

1. Simple Sentence Answer
2. Unit Values
3. In A Geometry Question DRAW THE SHAPE
4. Whatever You Know Nothing About Is The Variable
5. Identify Your Variable
6. The Other Unknown Relates To The Variable


Those are the 6 steps for sucess.

Here's an example on how you solve an Algerbra problem solving question.
The question is "A farmer uses 54 metres of fencing to enclose a rectanguler field. If the width is two metres less than the length, find the dimensions of the field.


1. Simple Sentence Answer

For the simple sentence answer all you need is 3 words. Those 3 words are
The, are and whatever the question is asking you to find. So in this case your looking for the dimensions. So your simple sentence answer would be

The dimensions are _________ and _________


2. Unit Values

Unit values simply ask you to put whatever value you're working with in your simple sentence answer. So since we're working with metres you put "m" in your sentence. So it should now look like

The dimensions are _________m and _________m


3. In A Geometry Question DRAW THE SHAPE

This one pretty self explanitory


4. Whatever You Know Nothing About Is The Variable

For this one your variable(x or n or whatever you want) is the thing you have no clue about. So your first need to figure out who the playaz are. So the playaz are length, width and the perimeter. We know already know that the perimeter is 54 metres so it can't be the variable. We also know that the width is 2 metres less than the length so that leaves us with length which we know nothing about. So length is the variable.

length= variable


5. Identify Your Variable

I don't really understand this step but I think this is the one were we have to remember to put let x= length somewhere or we lose a half a mark. So add
x= length

6. The Other Unknown Relates To The Variable

I dont really understand this one but I think it means if you have two unknowns they relate to the variable.


After all 6 of those steps you can finally start doing your work.
So all that was just an explanation on the steps. Now to get to the point of this scribepost. So the side I'm doing is the geometry side. The side that has the title
What's the Quickest Way for an Ant to Go From the Ground to the Tree Trunk

Questions


1. The length of a rectangle is 3 times the width. The perimeter is 96 cm. Find the width and length.

2. The length of a rectangle us 5m greater than the width. The perimeter is 150m. Find the width and length

Jonah's Scribe

Today in class...

We went over the homework to see if we had any questions about it and solved it together. Then we learned how to solve a 2 Step Equation. Here are the steps:
1. Isolate the variable
2. cancel the constant (integer) using its composite to make zero pairs.
3. Balance
3a. cancel variable to (1.)
4. Substitute to check.

Here is an example:


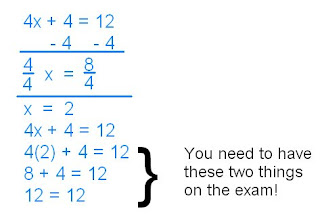
But, we didn't just learn how to show in that way. We also were shown how to show it by using Algetiles. Here is the example used in class:

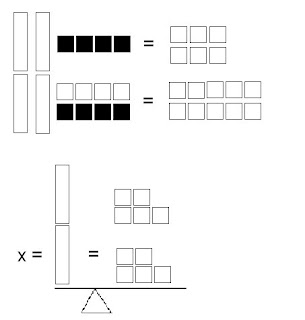That is how we use Algetiles to show 2 Step Equations! That is all we did in class. don't forget to do the homework we got.

Jordan's Scribe Post

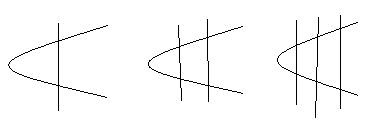First, we started with 3 patterns:Then we had to find the next 2 patterns, which were:
Then we had to make a T-Chart for the patterns we found...
the numbers in the "y" row start at 1 and go up by 2 each time..

the numbers in the "x" row start at 0 and go up by 1 each time..

to get "y," you have to multiply "x" by 2, then add 1

Algebraic expression: y = 2n+1

We started off with 3 different patterns this time... The 5 pictures looked like this:
(btw, the vertical lines through the strings are the cuts)
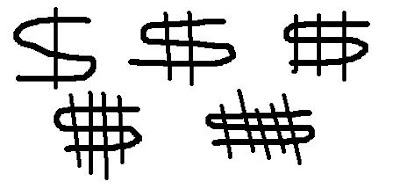Followed by the T-Chart:
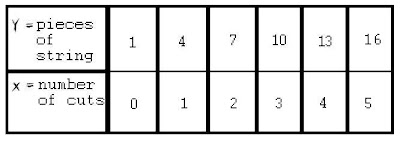We found that the "y" row started @ 1 then increased by 3 each time
We found that the "x" row started @ 0 then increased by 1 each time
You have to multiply "x" by 3 then add 1 to get "y"
Algebraic Expression: y = (3n)+1

THE END.

Marina's 2nd Scribe Post

My Scribe

Okay today in class, I volunteered to do a scribe post. I made a little slideshow on voicethread, i dont really know if i did it right so yeah...
P.s. I did this all on piant,so it ,might be messy.. didnt take me very long.



-marina☺☻○•

Robby's Scribe

Collecting Like Terms
Like terms are Terms that have the same Variables next to them. Variables are letters that stand for unknown or given numbers. Like terms are 2 or more terms that can be combined to simplify the equation. Lets look at an example:






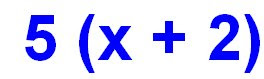
This right now is an algebraic math sentence. In algebra, you don't always have to find an answer to the question, that is, if you aren't told what the variable stands for. This is one of those occasions.
In algebra, you don't use all the operators you would use for non-algebraic equations. Like, for example, times (x). Because times has a operator that looks like a variable, it gets confusing (Like so: Variable x X x = x ...no it's not what you were thinking). So they removed it (they being those math geniuses that invented algebra). Instead of writing 5 x (x+2), you remove the x and assume its multiplication. And when multiplying a number with a variable, you write them next to each other (5x). This becomes a Term.
Back to the math sentence in blue above. An easy way when multiplying things in brackets and theres a variable in there is to multiply the outside number with the variable. So it would look something like this:







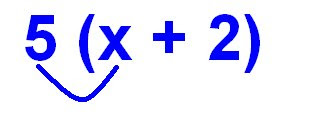
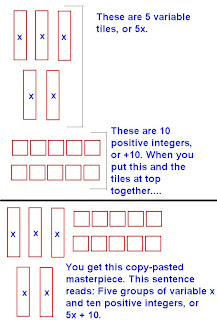
Like I said before, when multiplying a number with a variable, you put the variable on the right side of the number and it becomes a term. So 5x means Five groups of variable x.
The next part of the question is the +2. You would read this as positive two, because in algebra, you deal with integer numbers a lot. Now you have to multiply it with 5 now, because its still in the brackets, and if there's no operator between the brackets and number on the outside, you assume its multiplication.








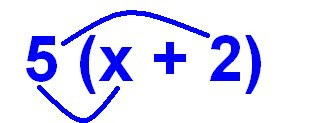
Now, we multiply the 5 with the 2. 5 x 2 = 10 (note, I used the x symbol for multiplying because we aren't multiplying the terms, and this equation won't go in the final answer, only the 10 will)
The math sentence now looks like this:






This is a proper algebraic sentence. The terms should always be on the left side, and the non-terms, or integers, on the right. Now to to show you how to write this question using algebra tiles. But first, look at the different kind of shapes used to represent the parts of a algebraic-math sentence.




















Now that we know what shapes I'll be using mean, on with the algebra-sentence. I'll simply show what the simplified answer to the algebra sentence near the middle of my scribe-post looks like with algebra tiles...





=