Like terms are Terms that have the same Variables next to them. Variables are letters that stand for unknown or given numbers. Like terms are 2 or more terms that can be combined to simplify the equation. Lets look at an example:
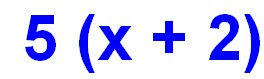
This right now is an algebraic math sentence. In algebra, you don't always have to find an answer to the question, that is, if you aren't told what the variable stands for. This is one of those occasions.
In algebra, you don't use all the operators you would use for non-algebraic equations. Like, for example, times (x). Because times has a operator that looks like a variable, it gets confusing (Like so: Variable x X x = x ...no it's not what you were thinking). So they removed it (they being those math geniuses that invented algebra). Instead of writing 5 x (x+2), you remove the x and assume its multiplication. And when multiplying a number with a variable, you write them next to each other (5x). This becomes a Term.
Back to the math sentence in blue above. An easy way when multiplying things in brackets and theres a variable in there is to multiply the outside number with the variable. So it would look something like this:
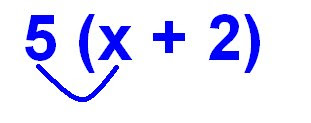
Like I said before, when multiplying a number with a variable, you put the variable on the right side of the number and it becomes a term. So 5x means Five groups of variable x.
The next part of the question is the +2. You would read this as positive two, because in algebra, you deal with integer numbers a lot. Now you have to multiply it with 5 now, because its still in the brackets, and if there's no operator between the brackets and number on the outside, you assume its multiplication.
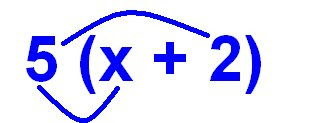
Now, we multiply the 5 with the 2. 5 x 2 = 10 (note, I used the x symbol for multiplying because we aren't multiplying the terms, and this equation won't go in the final answer, only the 10 will)
The math sentence now looks like this:

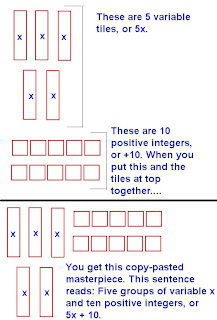
This is a proper algebraic sentence. The terms should always be on the left side, and the non-terms, or integers, on the right. Now to to show you how to write this question using algebra tiles. But first, look at the different kind of shapes used to represent the parts of a algebraic-math sentence.

Now that we know what shapes I'll be using mean, on with the algebra-sentence. I'll simply show what the simplified answer to the algebra sentence near the middle of my scribe-post looks like with algebra tiles...

=


1 comment:
I like how you explained your scribe. It was easy to read and i would know what to do if i missed a day in class.
Post a Comment