Kiahna's 2nd growing post

Question #2

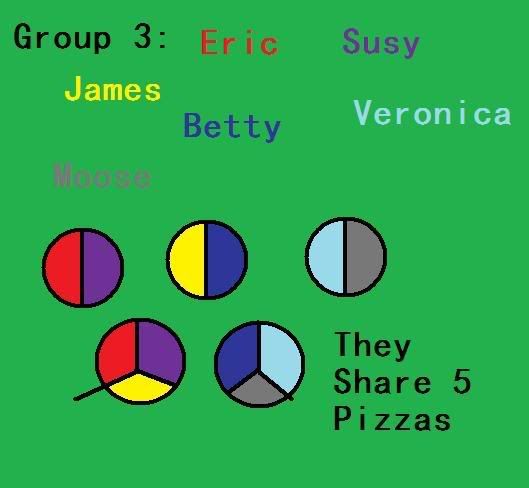
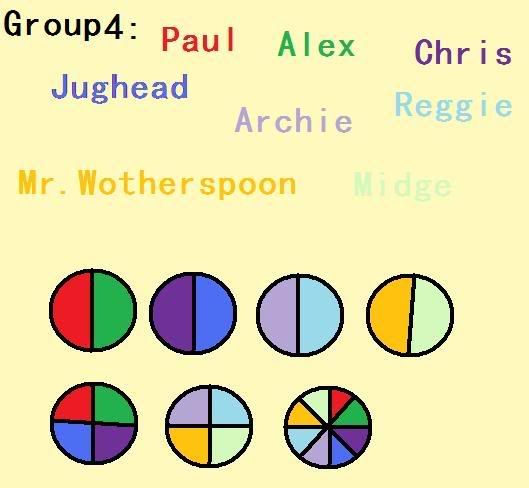
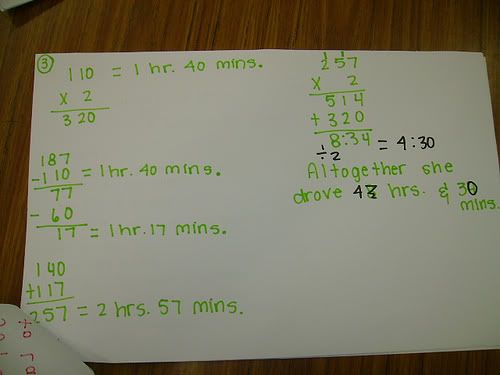a.What strategies were nedded?
well there was ratio tables that was probably the best one to use. You could have also used clocks and money or maybe even number lines. You also could have used adding subtracting division and multiclipation maybe.

b. How did you use these strategies?
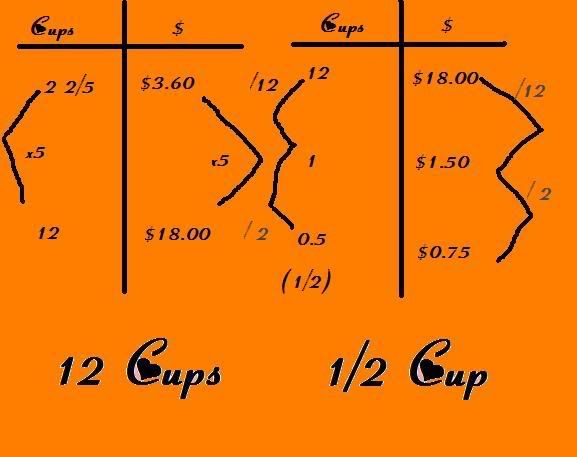
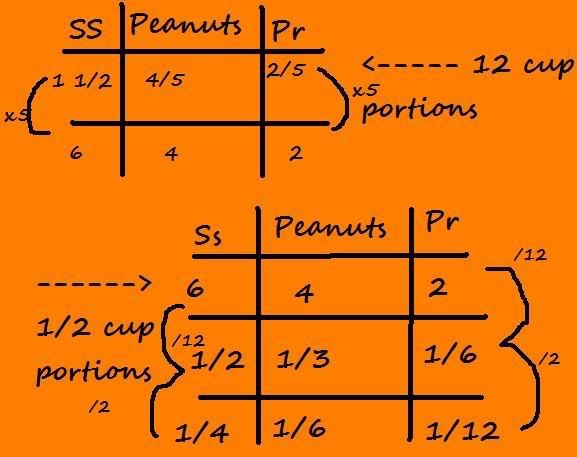
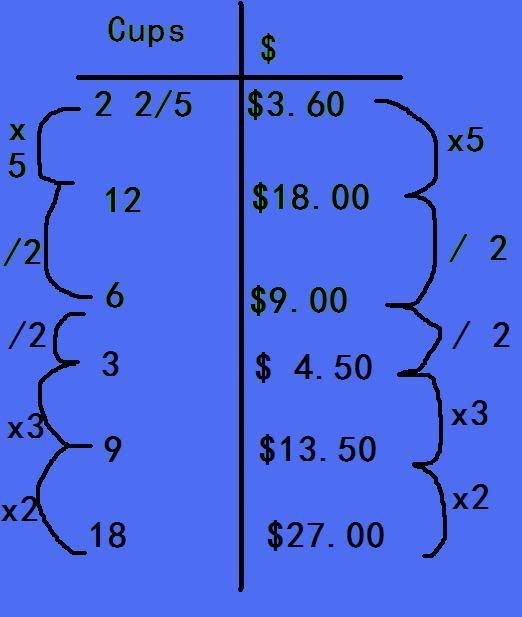
well i used a ratio table, i had one side fractions and the other side money. i times one by whatever number went into both sides and that is what i did.







c. How could i have used the strategies?



Well im not to sure if you could use money for this but you probably could. It could be an easy way to find the price of each ingredient. I dont tink clocks would be the best way to go you should just stick to ratio tables.







d. This is how i got six i just divides 12 by two to get 6 because 6 is half of 12.






e. i used 3, 1 1/2, 3/4 because that is just dividing it by 2 the whole time.




Question #2










1. 2/3 + 1/4 + 2/5=
2/3 is 40minutes
1/4 is 15 minutes
2/5 is 24 minutes. (i made a mistake on my paper for that one)
so the answer is 79/60 which is 1 19/60.

2. 6/5 can change into 1 1/5 which is $1.20 cents 11/10 is 1 1/10 which is also $1.10 so if you subtract that you will get 10 cents which is also 1/10

3. 3/5+2/7=31/35
i used a # line out of 35 and 2/7 of 35 is 10 and 3/5 of 35 is 21 and if you add that you will get 31/35

4. 1/6+1/9 is 5/18
i used a # line out of 18 1/6 of 18 is 3 and 1/9 of 18 is 2 so that is 5/18 together. '

3rd Question

the comments didn't work




-i used strategies like ratio tables, equivalence means that they are equal, measurments, the whole matters, partial products and friendly fractions.
-You use these strategies to make the work easier. instend of using dividing and multiplication you can use these.
-i did all the other questions on the paper.




QUESTION # 4






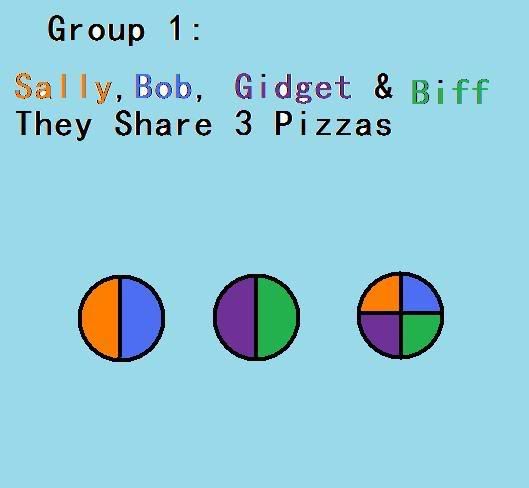
(on the first question i made a mistake each person should get 3 pieces ans for the 2nd way it would be 45 minutes sorry also for the 3 question the f stands for five)
-the group that gets the largest portion was is all the group one because they get the largest pieces. They may have the least amout of pieces but they stilll have the bigggest pieces.
-For my strategies i used dividing and clocks.
- for question 1,3,5 on the sargent park math zone website. Those were done on my paper on the voice thread.

Growing Post Question 1 Betty's Snack Mix Total (15 marks) 15/15
Answers all questions 5 marks (1 per Question) 5/5
Quality of Answers 10 marks 10/10

Growing Post Question 2 (10 marks) 10/10

Embeds the voicethread after question 1 (1 mark) 1/1
Creates the Voicethread to answer Question (1 marks) 1/1
Add Comments to further elaborate on the strategies used 4/4
Max 4 marksMath work is correct in the voicethread (4 Marks) 4/4
Bonus marks for any person doing more than 4 questions (2 marks) 2/2

Growing Post Question 3 (14 marks) 13/14
Uses Pictures or a voicethread to answer the question (3.5 Marks) 3.5/3.5
Explains the 7 strategies using 7/8 and 11/12 (7 Marks) 6/7
Comments on the voicethread (3.5 marks .5 per comment) 3.5/3.5

Question 4 Sharing Pizza's (15 marks) 13/15
Clearly shows How much pizza does each student get in the different groups?4/4
Shows which group gets the largest portion of Pizza (2 marks) 2/2
Show how you found your answer in 2 different ways. (4 marks) 3/4
What strategies did you use in finding your answer. Student must show strategy and explain how it was used.(2 marks) 2/2
Added comments on voicethread or added detail to explanations (3 marks) 2/3
Total Math Work (54 marks)

Formatting (31 Marks) 31/31

Proper title (2 Marks) 2/2
Proper labels (3 marks) 3/3
Only one post and no drafts left in dashboard (2 marks)2/2
Questions are in the proper order (4 Marks)4/4
Post looks pleasing (10 Marks) 10/10
Pictures are lined up, text is left justified etcThe post looks professional and not piecemeal.Completing Self Evaluation and leaving a comment (10 Marks) 10/10

Completing 2 Peer Evaluations Leaving comments on the Growing Post and Voicethreads (20 marks) 20/20
10 marks per student

Total Marks for Growing Post ( 105 Marks) 102/105 that is what i got.

i think i did a pretty good job on the second growing post. i knew what i was doing and im glad that i finished it on time. ALL DONE!!!!!!!

Danica's 2nd Growing Post

Question 1 Use this picture and reflect on your the puppy kibble test.
What strategies were needed?

The strategies that were needed are: A ratio table, money, clocks, and double number lines.
How did you use these strategies?

I used money and clocks.
Or How could you of used these strategies.

I could have used a ratio table which would have made my work neater and easier.
How would you figure out the price of a 6 cup bag of Betty's Snack mix? Use a ratio table

Find 3 other values (amounts of Snack Mix) that could be solved using the same ratio table. Find the $$ of your new container sizes.

wmode="transparent">

Scoring Sheet That I Will Mark Myself On!

Growing Post Question 1 Betty's Snack Mix Total (15 marks)= I give myself a 15 / 15 because i answered all the questions to the best of my ability.

Answers all questions 5 marks (1 per Question)

Quality of Answers 10 marks

10= Perfect

8= Great Job but there is room for improvement

7=Good Job but there is much room for improvement

6= Decent job but you need to work harder

5= All work is done but effort is lacking

Less than 5 would be for questions answered incorrectly and without effort and incomplete.

Growing Post Question 2 (10 marks)= I give my self a 10/10 because i answered all of the questions you asked us to mark ourselves on.

Embeds the voicethread after question 1 (1 mark)

Creates the Voicethread to answer Question (1 marks)

Add Comments to further elaborate on the strategies used (1 per comment left) Max 4 marks

Math work is correct in the voicethread (4 Marks)

Bonus marks for any person doing more than 4 questions (2 marks)

Growing Post Question 3 (14 marks)= i give my self a 13/14 because i think i could have explained my answers alittle better.

Uses Pictures or a voicethread to answer the question (3.5 Marks)

Explains the 7 strategies using 7/8 and 11/12 (7 Marks)Comments on the voicethread (3.5 marks .5 per comment)

Question 4 Sharing Pizza's (15 marks)= i give my self a 15/15

Clearly shows How much pizza does each student get in the different groups? (4 marks)

Shows which group gets the largest portion of Pizza (2 marks)

Show how you found your answer in 2 different ways. (4 marks)

What strategies did you use in finding your answer. Student must show strategy and explain how it was used.(2 marks)

Added comments on voicethread or added detail to explanations (3 marks)

Total Math Work (49 marks)

Formatting (21 Marks)= i give my self a 54/54 because all my work is up to your standards.

Proper title (2 Marks)

Proper labels (3 marks)

Only one post and no drafts left in dashboard (2 marks)

Questions are in the proper order (4 Marks)

Post looks pleasing (10 Marks)

Pictures are lined up, text is left justified etc

The post looks professional and not piecemeal.

Completing Self Evaluation and leaving a comment (10 Marks)

Completing 2 Peer Evaluations Leaving comments on the Growing Post and Voicethreads (20 marks) 10 marks per student

Total Marks for Growing Post ( 100 Marks)=i get a 104/105

Growing Post Completed on time 0 mark deduction

Completed 1 day late 10 mark deduction

Completed 2 Days Late 15 Mark Deduction

Completed more than 2 days late 20 Mark Deduction

I commented on Kiahna's and Andrea's growing posts.

Robby's 2nd Growing post

Question 1: 1)What strategies were needed?
-I used a Ratio table, maybe some money strategies, and division and multiplication between both answers
2)How did you use these strategies?
-For the multiplication and division between both answers part, to get 1/2 cups, I answered 12 cups by multiplying 2 2/5 (2.4) by 10 to get 24, then divide it by 2 to get 12. Then I divided 12 by 12 and then by 2 to get 1/2.
( 2.4 x 10 = 24 ÷ 2 = 12 cups 12 ÷ 12 = 1 ÷ 2 = 1/2 cups. *Then do same strategy for the ingredients and price.)
-The ratio table was basically the same information as the multiplication and division part, but with a visual aide and a little neater

3)Or How could you of used these strategies.
-The Money Strategy
-I would have used a money strategy, but it just asked you to find how much it costed, not how many pennies, nickles, and dimes you would need to give Betty to buy her snack mix. So in short, this strategy didn't really help, wouldn't get extra marks for because it didn't answered any questions, and would just be a waste of time.
4)How would you figure out the price of a 6 cup bag of Betty's Snack mix? Use a ratio table
-To get 6 cups, I would multiply the cups and price for a 2 2/4 container by 10, then divide the answer by 2, then divide it by 2 again to get 6 cups.











5)Find 3 other values (amounts of Snack Mix) that could be solved using the same ratio table. Find the $$ of your new container sizes.

-The 3 others are circled in green. For the price of 3 cups, I added the price of a 1 cup and 2 cup container to get it.

Question 2:

Vina's Scribe

Today and yesterday we were in groups of 2, we were trying to figure out if Mark and Rachel ran more than last year. I figured it out by dividing the total miles (26) to total water stations (8) which = 3.2 then i times 3.2 to 5 = 16. So now i know mark ran 15 miles. Then i divided total miles (26) to total flags (12) = 2.2 then i multiplied 2.2 to 7 = 15.4 then i rounded 15.4 = 15. I also now know that mark ran further than Rachel. I figured out if the fourth water station is the half of the course by looking at the map.



VinaSarmiento&JordanPabon'swork™©

Jordan's 2nd Growing Post

QUESTION 1 pt. 1: What strategies were needed?
answer: We needed to use ratio tables to figure out how to get the amount of ingredients for the different sized cups. We also could have used double number lines to figure out fractions!

QUESTION 1 pt. 2: How did you use these strategies?
answer: I used the ratio tables to get the amount of ingredients for 12 cups and 1/2 of a cup.

QUESTION 1 pt. 3: How could you use these strategies?
answer: I could have also used ratio tables to solve the rest of the questions but I wanted to have some variety
QUESTION 1 pt. 4: How would you figure out the price of a 6 cup bag of Betty's Snack mix? Use a ratio table.
QUESTION 1 pt. 5: Find 3 other values that could be solved using the same ratio table.
( I combined pt. 4 with pt. 5 )

QUESTION 3: Write and use pictures to describe how you would uses those strategies to explain how far the two students would have run if Mark ran 7/8 and Rachel ran 11/12 of the RACE course.

Explain using:

Equivalence
Fractions show operations
Ratio Tables (Proportional Reasoning)
Measurement
Partial Products or the Distributive Property
The Whole Matters
Friendly Fractions

write and use pictures to describe how you would uses those strategies to explain how far the two students would have run if Mark ran 7/8 and Rachel ran 11/12 of the RACE course.

QUESTION 4

in group 1, the kids get 3/4 of a pizza, in group 2, they get 4/5, in group 3, they get 5/6, in group 4 they get 7/8.

since 7/8 > 3/4, 4/5, and 5/6, group 4 got the most portions

i used ratio tables and a formula to answer the questions.

blah. harbeeck >_>
MERRY CHRISTMAS! ...and a happy new year!!
-the PABON(:

SELFEVAL~
Growing Post Question 1 Betty's Snack Mix Total (15 marks)

Answers all questions 5 marks (1 per Question) 5/5

Quality of Answers 10 marks 9/10

10= Perfect
8= Great Job but there is room for improvement
7= Good Job but there is much room for improvement
6= Decent job but you need to work harder
5= All work is done but effort is lacking
Less than 5 would be for questions answered incorrectly and without effort and incomplete.

Growing Post Question 2 (10 marks)

Embeds the voicethread after question 1 (1 mark) 1/1
Creates the Voicethread to answer Question (1 marks) 1/1
Add Comments to further elaborate on the strategies used (1 per comment left) Max 4 marks
4/4
Math work is correct in the voicethread (4 Marks) 4/4

Bonus marks for any person doing more than 4 questions (2 marks) n/a

Growing Post Question 3 (14 marks)

Uses Pictures or a voicethread to answer the question (3.5 Marks) 5/5
Explains the 7 strategies using 7/8 and 11/12 (7 Marks) 7/7
Comments on the voicethread (3.5 marks .5 per comment) if we need the . . . . . . voicethread , 0/5. if we dont 4/5

Question 4 Sharing Pizza's (15 marks)
Clearly shows How much pizza does each student get in the different groups? (4 marks) 3/4
Shows which group gets the largest portion of Pizza (2 marks) 2/2
Show how you found your answer in 2 different ways. (4 marks) 4/4
What strategies did you use in finding your answer. Student must show strategy and explain how it was used.(2 marks) 2/2
Added comments on voicethread or added detail to explanations (3 marks) 0/3 or 3/3

Total Math Work (49 marks)
46/49

Formatting (21 Marks)

Proper title (2 Marks) 2/2
Proper labels (3 marks) 3/3
Only one post and no drafts left in dashboard (2 marks) 2/2
Questions are in the proper order (4 Marks) 4/4
Post looks pleasing (10 Marks) 9/10

Pictures are lined up, text is left justified etc

The post looks professional and not piecemeal.

Completing Self Evaluation and leaving a comment (10 Marks) 10/10
Completing 2 Peer Evaluations Leaving comments on the Growing Post and Voicethreads (20 marks) 10 marks per student 18/20

Total Marks for Growing Post ( 100 Marks)

FINAL MARK 94/100

Growing Post Completed on time 0 mark deduction
Completed 1 day late 10 mark deduction
Completed 2 Days Late 15 Mark Deduction
Completed more than 2 days late 20 Mark Deduction

Danica's scribe

Today we were doing this thing where we used a ratio table
and a box picture to find out the answer to a problem. What i did to find out the answer another was 36 divided by the denominator of the fraction.

Chantel's 2nd Growing post

Questions (1):

1. What strategies were needed?

2. How did you use these strategies?

3. Or How could you of used these strategies.

4. How would you figure out the price of a 6 cup bag of Betty's Snack mix? (Use a ratio table)

5.Find 3 other values (amounts of Snack Mix) that could be solved using the same ratio table. Find the $$ of your new container sizes.

Answers:

1. The stategies that I think that were needed was the ratio table stratgy beacuse I think it's very easy to use ratio table. it's easy because what you do to one side you have to do to the other. So like the lazy teenager I am I used that strategy. I also used all this math work but I then showed it on a ratio table because it looked neater!!

2. I used these strategies for showing how I got 12 cups , 1/2 cup and the prices.
I also used it to show the portions. As you can see in the pictures below.







3.I don't know any other ways that I could of used this stratgy.

4. I could find the price for 6 cup bag of Betty's Snack Mix by using a ratio table and doing the same thing to one side as I did to the other. Also I could use 12 beacuse I already know that then divide it by 2 to get 6.




5. Here I found three other values using the same ratio table.







Question 2:
Its The First Four Slides/Pictures.












Question 3:
Its Slide 6-11






Question 4:



Everyone In This Group Gets an Half And 1/4

Everyone gets 4 pieces of pizza.


Everyone in this group gets an half and 1/3



Everyone gets and half and 1/4 and 1/8.

kiahna's scribe

1.for the first question:
i used a ratio table to figure out the price.

2.I used a ratio table to get the portions

For the second question I again used a ratio table.

I started at twelve cups i just skipped a step.




For the portions of the ingredient i again used a ratio table.

Robby's Scribepost

The steps I would take....

STEP 1:
Write down the information:

For a 2 2/5 cup container, there are:
-1 1/5 cups of Spicy Shreddies
-4/5 of a cup of Peanuts
-2/5 of a cup of Pretzels

She wants to sell a 12 cup container and a 1/2 cup container using this information to scale.






STEP 2:
Make a table using Cups and Price to find a rule.

THE RULE:
x10 and ÷2


















STEP 3:
Use the rule we found in Step 2 for the decimal form of the quantity of Peanuts, Pretzels, and spicy Shreddies in cups to make it to scale:

1 1/5 (Spicy Shreddies) = 1.2
4/5 (Peanuts) = 0.8
2/5 (Pretzels) = 0.4
------
2.4 (2 2/5)

Now multiply all the decimals by 10 and divide by 2 to get the amount needed for 12 cups.

1.2 x 10 = 12

12 ÷ 2 = 6 cups of Spicy Shreddies for a 12 cup container

-----------------
0.8 x 10 = 8

8 ÷ 2 =4 cups of Peanuts for a 12 cup container

----------------
0.4 x 10 = 4

4 ÷ 2 = 2 cups of Pretzels for a 12 cup container

For a 12 cup container, there will be:
-6 cups of Spicy Shreddies
-4 cups of Peanuts
-2 cups of Pretzels
And the price will be $18.00 (as shown on table above).



The good way to get 1/2 cup is to redo the strategy above, finding rules and such. But another way you could do it is to use the information given on 12 cups, and divide it by 12 then 2 [(12 ÷ 12 = 1 ÷ 2 = 0.5 (1/2)].

So:

-6 cups ÷ 12 = 0.5 (6 goes into 12 2 times, so 12 goes into 6 0.5 times, or 6 is half of 12) - 0.5 ÷ 2 = 0.25 cups (1/4) of Spicy Shreddies ------
0.5
-4 cups ÷ 12 = 0.3 (4 goes into 12 3 times (1/3), so 12 goes into 4 0.3 times, or 12 is 3.3 repeater (1/3 as a decimal) times bigger than 4)
-0.3 ÷ 2 = 0.175 cups of Peanuts
-------
0.5

-2 cups ÷ 12 = 0.16 (2 goes into 12 6 times (2 / 12 = 1/6), 6 ÷ 100 is 0.16. So 1/6 (2/12) = 0.16 as a decimal)
-0.16 ÷ 2 = 0.08 cups of Pretzels
-------
0.5

Now the Price:
$1.50
----------
$18.00 ÷ 12 = 12 | $18.00
12.00
---------
6 (0)
60
------------
0



SO:
For a 1/2 cup container, there are:
-0.25 /0.5 cups of Spicy Shreddies
-0.175 / 0.5 cups of Peanuts
-0.08 / 5 cups of Pretzels

And the price is $1.50






P.S.
Sorry for the Late Scribe, heh my bad.
Oh and Long division with computers SUCKS. Stick with the simple equations to those of you who will copy this idea.

David's Scribepost

The test that we did on Wednesday November 21, 2007.

The question! was just like the one where we needed to make the label for the Maria's Puppy Kibble.

It said that Betty wanted to make new containers for her snack mix. Her original size was 2 2/5 cup containers. They had 1 1/5 of spicy shreddies, 4/5 of peanuts, and 2/5 of pretzels, for $3.60. The question was to make new labels for her new containers of 12 cups and 1 cup, and to label the ingredients, the amount of the ingredients, and the price of the package.

The Strategy! I used to find out how much shreddies, peanuts and pretzels were in each container was the ratio tables where what ever you did to one side, you do to the other.

The Work!

As you can see on the ratio table, I found out what 12 cups was first. To get 12 cups I turned 2 2/5 into 12 by multiplying it by 5. then multiplied the rest by 5 to make them equal proportions. THEN, I divided the answer for 12 cups, by 12 to get it to one (and the other stuff because whatever you do to one side of a ratio table you do to the other). Now that we have one, we can turn that into anything! So i divided it again, but this time by 2 because 2 parts of 1 is a half. Then i just filled in the information that we got here, into the label! Just like that easy marks =]

* SCRIBE POST FOR DAVID IS DONE!!!! *

Sorry i didn't do this yesterday, but i fell asleep . . . Yeah.

Nathaniel's Scribepost

Maria's Big Trip.

We had to figure out the answers to these questions:
1) How many gallons of gas and what fraction of a full talk of gas did Maria use on the turnpike driving from her house to Lance's house?
2) What fraction of the full tank of gas did she use on the turnpike driving from her house to Lance's to Alicia's house?
3) How much time will she spend driving on the turnpike when she drives back home to Philadelphia

What information was given already?
1) There are mileage markers that stretch across the state like a giant number line. (Starting from zero on the west and increasing to the right.)
2) Maria gets 33 miles per gallon.
3) Maria's house is at mile marker 352
4) Lance's house is at mile marker 242
5) Maria's to Lance's took 1 hour and 40 minutes. (or 100 minutes)
6) Alicia's house is at mile marker 55















Answer to Question One.
First we figured out how much miles between Maria's and Lance's house was. We did that by subtracting the mile markers. 352 - 242 = 110 Miles. So between them was 110 miles. On the gas gauge, 110 miles is between 3 gallons and 4 gallons of gas, so the gas is 3 and something. Each gallon was 33 miles, so in between 3 gallons and 4 gallons is 33 miles, so 110 miles is 3 ?/33
Since 3 gallons is 99 miles, we subtracted 110 by 99 and got 11. So its 3 11/33 and you can change that into 3 1/3 of a tank of gas from Maria's to Lance's.

Answer to Question Two. (messed up on the paper thought 287 was 297 -.-)
First we figured out the miles from Maria's to Alicia's. Since we already figured out that from Maria's to Lance's was 110 miles, we just had to figure out Lance's to Alicia's. So we subtracted Lance's mile marker by Alicia's. 242 - 55 = 187 Miles. So it was 187 miles from Lance's to Alicia's. We added both up (187 + 110 = 287 miles) and in total from Maria's to Alicia's it was 287 miles. On the gas gauge it said that it was between 8 gallons (269 miles) and 9 gallons (297 miles) So we subtracted the total miles with 8 gallons (287 - 269 = 18) so its 8 18/33 gallons in total.

Answer to Question Three.
To do this we used a Ratio Table. We used the information from Maria's to Lance's. (110 miles / 100 minutes) Then we subtracted how far from Lance's to Alicia's with Maria's to Lance's. (187 - 110 = 77 miles. Since it was divisible by 11 we divided 110 miles by 10 and the minutes to get 11 miles. (110 miles / 10 = 11 miles) (100 minutes / 10 = 10 minutes) So now we have 11 miles and 10 minutes. Now we just multiplied by 7. (11 x 7 = 77 miles) (10 x 7 = 70 minutes) Then we added the 110 miles with it to get 187 miles. (110 + 77 = 187 miles) (100 + 70 = 170 minutes) So that that was from Lance's to Alicia's now we just add Maria's to Lance's (187 + 110 = 297 miles) (170 + 100 = 270 minutes) So the whole thing took Maria 270 minutes or 4 hours and 30 minutes.

Andrea's Scribe Post

The Pennsylvania Turnpike Investigation

Maria is going on a big trip to go see her friends Lance and Alicia. Lance lives in Harrisburg and Alicia lives outside of Pittsburgh.

These were the three questions we had to answer during this investigation:

1.) How many gallons of gas and what fraction of a full tank of gas did Maria use on the turnpike driving from her house to Lance's house?

2.) What fraction of the full tank of gas did she use on the turnpike driving the combined distance from her house to Lance's to Alicia's house?

3.) How much time will she spend driving on the turnpike when she drives back homw to Philadelphia?

Work Sheet Facts:

- 33 miles per gallon

- 15 gallon tank

- Exists 242 on turnpike

- On the road for 1 hr. 40 minutes

- Drives from Lance's house to Alicia's

- Maria then exists off on mile marker 55

We then took 352 which was the mile marker she get's on.Then we took 242 which was the mile marker she got off of. We subtracted them both and it = 110.

Then we figured out how many 33's go into 110 because that is how many miles she can drive per gallon.

Ratio Table:

Miles Gallons

33 1

66 2

99 3

We subtracted 99 from 100 and it = 11. We used 99 because that is the closest number to 100. If 33 = 1 gallon then 11 is 1/3 of a gallon. Maria used 3/15 and 1/3 of a gallon.

For number two we subtracted 55 from 242 and it = 187. We used 242 because that is the mile marker she got on.

Ratio Table:

Mile Gallons

33 1

66 2

99 3

132 4

165 5

Then we subtracted 165 from 187 which =22. Since 11 is 1/3 of 33 therefore 22 is 2/3 of 33 because 11 is half of 22, so you can just double it. You double everything!

Next Question:

What fraction of the full tank of the gas did she use on the turnpike driving the combined distance from her house to Lance's to Alicia's?

So we then added 3/15 & 1/3 +5/15 & 2/3
So 1/3 +2/3 = one whole
Then i go 3/15+5/15 which equals 8/15but we have to add the whole there fore it would be 9/15
So she used 9/15 from her house to Lance's To Alicia's

For number three we tried to see how many times 110 can go into 140. 140 = 1 hr. and 40 mins.

We multiplied it by 2 and got 220. Then we took 110 and subtracted it from 187 = 77. 77-60 =17. That = 1 hr and 17 mins. Then we took both of the hours 140 + 117 =257. 2 hrs. and 57 mins. Then we multiplied 257 x 2 =514 +320 which = 834. 8 hrs. and 34 mins. Then we divided that by 2 because the question only asked for going back and not there too. That = 4 hours and 30 mins. Altogether Maria drove 4 hours and 30 minutes.

-Andrea :p

Chantel's Scribepost

The Pennsylvannia Turnpike Investigation

We are doing an investigation involving Maria and her drive to Lance's and Alicia's house. There is three questions we had to answer.

1. How many gallons of gas and what fraction of a full tank of gas did Maria use on the turnpike driving from her house to Lance's house?

2. What fraction of a full tank of gas did she use on the turnpike drving the combined distance from her house to Lance's to Alicia's.

3. How much time will she spend driving on the turnpike when she drives back home to Philadelphia?

Here Is Some Info That We Got On The Work Sheet

-33 miles per gallon

-15-gallon gas tank

-Gets on at mile marker 352

-She then exits on mile marker 242

-She has now been on the road for 1 hour and 40 minutes

-Now she drives from Lance's to Alicia's

-She now exits and mile marker 55

1.

We took 352 (the mile marker she ghets on the road) and subtracted 242 ( The mile marker she got off). We then got 110. We then had to see how mant 33's would go into 110. We did that because 33=1 gallon.

MileGallon

-----------

33 1

66 2

99 3
Then we subtrated 110 by 99 ( beacuase 99 is the closet thing to 100). Then we 11. 33 is one gallon so 11 is 1/3 of a gallon.So She Used 3/15 and 1/3 of a gallon.

2. For number 2 we went 242 ( The mile marker she got on) and subtratced that by 55. We then got 187.

MileGallon

-----------

33 1

66 2

99 3

132 4

165 5

Then we took 187 subtracted it by 165 and we got 22. Since 11 is 1/3 of 33 therefore 22 is 2/3 of 33.

Thats all we did.

But I read over the question and it says that What fraction of the full tank of the gas did she use on the turnpike driving the combined distance from her house to Lance's to Alicia's?

So we have to now add 3/15 & 1/3 +5/15 & 2/3

So 1/3 +2/3 = one whole

Then i go 3/15+5/15 which equals 8/15but we have to add the whole there fore it would be 9/15

So she used 9/15 from her house to Lance's To Alicia's

3. Ohkay well I really didn't understand what we did for number three.

I really don't kno whow to explain it.

Sry about the inconvenience.

♥.:;Chantel;:.♥

~xoxo~xoxo~